Area Estimation for Images with Defined Edges

This fourth activity is about area measurement.  Using Green's Theorem, the area of a defined contour can be obtained.  Green's Theorem says that the line integral of the boundary is equal to the area enclosed within that boundary. 

Using Paint, I created shapes of rectangle, square, and right triangle.  The background is color black, white for the shapes.  To know analytically the area of the shapes, I obtained the pixel coordinates of the edges. When counting for the pixel coordinates of the shape, consider only the white part of the image.  Using the formula for the area of these shapes, then we have the analytical area.  Below are the shapes I made, formulas for the area and the summary of the analytical area:

Figure 1 (a)

Figure 1 (b)

Figure 1 (c)

Figure 1.  Different shapes created using Paint.

Rectangle: A = Length*Width                    (1)

Square: A= Side*Side                               (2)

Right triangle = (1/2)(Base*Height)          (3)

            Table 1. Analytical areas of different shapes.

	x1	y1	x2	y2	Length/Base	Height	Area
rectangle	104	103	299	198	195	95	18525
square	58	60	248	250	190	190	36100
triangle	72	39	272	262	200	223	22300

Note that the computed area are in terms of square pixels.

Now, let us compute for the area using Green's Theorem.  Using Scilab, load the image with the function 'imread'.  Then, get the contour of the shape using the function 'follow'.  This function obtains the coordinates of the border of the image.  It treats the '0' (black color) as background and the '1' (white) as the object.  This is the reason why when counting for the pixel coordinates of the object, one must consider only the white part.

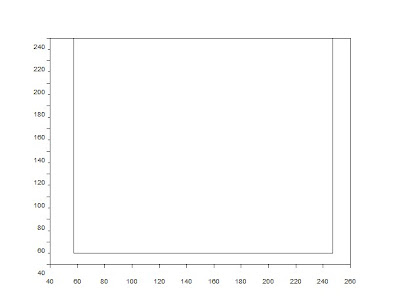
To check whether I got the correct set of coordinates, I plotted the values and are shown below:

Figure 2 (a)

Figure 2 (b)

Figure 2 (c)

Figure 2.  Contour plot for rectangle (a), square (b), and right triangle (c).

Then, I implemented the Green's Theorem in Scilab (see code below).  Here is the summary of the results:

Table 2.  Summary of the results.    

Analytical	Result	% difference
18525	18525	0
36100	36100	0
22300	22288	0.054

The % difference from the estimation of the area of the right triangle could be attributed to the slight deviation of its diagonal from being straight.

Figure 3.  Zoom in on the top part of the triangle.

Next, using Google Earth, I searched for the location of the Bahay ng Alumni.  Using the function printscreen, I pasted the image on Paint, as seen below:

Figure 4.  Aerial image of The Bahay ng Alumni (white part). 

I used the scale indicated on the map to convert the number of pixels in the image to its physical value.  The scale is:

145 ft = 259 pixels

1 square feet = 3.190535 square pixels

1square feet = 0.092903 square meter

Then, I edited the image in Paint.  I put a white layer on my object of interest, and then put a layer of black on the background that is close to the color white.  I do not have to color all of the background black. I could use the thresholding of the binary image conversion to rule out the background.  Below is the image of the edited version of the aerial view of the Bahay ng Alumni.

Figure 5. Edited image of the aerial view of the Bahay ng Alumni.

Then, on Scilab, I loaded the image and then converted it into grayscale.  Next, I converted it into a binary image with a threshold value of 1.  This would ensure that all of the background will be ruled out, as shown in Figure 5.

Figure 6.  Binary conversion of the edited image.

  

The area is obtained using the same method in computing for the area of different shapes.

 Table 3. Comparison of the area obtained to the area reported. 

	Land Area (square meters)	Computed (square meters)	% error
Bahay ng Alumni	3000	2912.851	2.90%

The error could be from missing some pixels that are included in the object of interest.  The aerial image of The Bahay ng Alumni is not that sharp, so the edges are not well defined. I could only approximate as to where the edges are.

I would like to thank Joseph Raphael Bunao for listening to my rants as to why my code is not working.  :)  This kept me thinking on how to debug my code.

I would give myself a score of 10/10 because I got all the expected output and my results are quite good (error is less than 5%).  Also, I debugged my code without direct external help.  I independently found out the problems on my code and corrected them.

I enjoyed doing this activity because I understood the concepts and I got fairly good results. :)

Code:

//area estimation

stacksize(10000000);

img = imread('C:\Users\May Ann\Documents\May Ann\Acads\5th Year 1st Sem\Image Processing\A4 Area Estimation for Images with Defined Edges\bahay_alumni1.bmp');   //load image

gray_im = im2gray(img);        //convert image to grayscale

bw = im2bw(gray_im, 1);        //convert grayscale into binary

imshow(bw);

imwrite(bw, 'C:\Users\May Ann\Documents\May Ann\Acads\5th Year 1st Sem\Image Processing\A4 Area Estimation for Images with Defined Edges\bahay_alumni1bw.bmp');

[x,y] = follow(bw);                // makes a matrix of points that defines the object.

N = length(x)                      // number of points on the border of the contour

scf()

plot2d(x,y);

//imwrite([x,y],'C:\Users\May Ann\Documents\May Ann\Acads\5th Year 1st Sem\Image Processing\A4 Area Estimation for Images with Defined Edges\bahay_alumni_plot.bmp');

//implementation of Green's theorem

N = length(x);

n = N-1;

i = 1:n

p = sum(0.5*( x(i).*(y(i+1)) - x(i+1).*(y(i))));

q = 0.5*(x(N).*y(1) - x(1).*y(N));

Area = p + q

References:

http://www.upalumni.ph/index.php?option=com_content&view=section&id=13&Itemid=56

http://www.metric-conversions.org/area/square-feet-to-square-meters.htm